双向链表 | eleven26

我们在单链表中，有了 next 指针，这就使得我们要查找下一节点的时间复杂度为 O(1)。可是如果我们要查找的是上一节点的话，那最坏的时间复杂度就是 O(n) 了，因为我们每次都要从头开始遍历查找。

为了克服单向性这一缺点，我们的老科学家们，设计出了双向链表。

双向链表（double linked list）是在单链表的每个节点中，再设置一个指向其前驱节点的指针域。所以在双向链表中的节点都有两个指针域，一个指向直接后继，另一个指向直接前驱。

// 线性表的双向链表存储结构
typedef struct DulNode
{
    ElemType data;
    struct DulNode *prior; // 直接前驱指针
    struct DulNode *next;  // 直接后继指针
} DulNode, *DuLinkList;

既然单链表也可以有循环链表，那么双向链表当然也可以是循环链表。

双向链表的循环带头节点的空链表如下图所示：

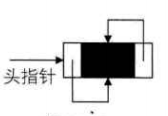
非空的循环的带头节点的双向链表如下所示：

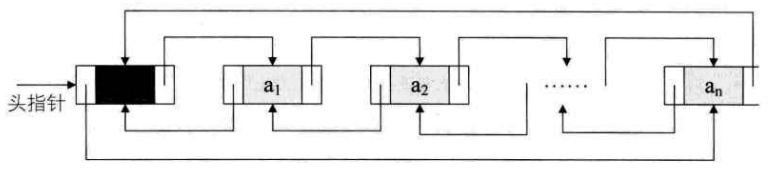
由于这是双向链表，那么对于链表中的某一个节点 p，它的后继的前驱是谁？当然还是它自己。它的前驱的后继自然也是它自己，即：

1	p->next->prior = p = p->prior->next;

双向链表是单链表中扩展出来的结构，所以它的很多操作和单链表相同，比如求长度的 ListLength，查找元素的 GetElem，获得元素位置的 LocateElem 等，这些操作都只涉及一个方向的指针即可，另一指针多了也不能提供什么帮助。

我们现在假设存储元素 e 的节点为 s，要实现将节点 s 插入到节点 p 和 p->next 之间需要下面几步：

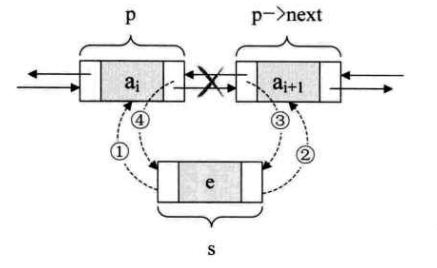
s->prior = p; // 把 p 赋值给 s 的前驱
s->next = p->next; // 把 p->next 赋值给 s 的后继
p->next->prior = s->next; // 把 s 赋值给 p->next 的前驱
p->next = s;  // 把 s 赋值给 p 的后继

总体来说，就是先正向连接起来，再反向连接起来。

关键在于它们的顺序，由于第 2 步和第 3 步都用到了 p->next。如果第 4 步先执行，则会使得 p->next 提前变成 s，使得插入的工作完不成。因为这样一来我们就没有办法找到原始的 p->next 了。所以我们不妨把上面这张图在理解的基础上记忆，顺序是先搞定 s 的前驱和后继，再搞定后节点的前驱，最后搞定前节点的后继。

若要删除节点 p，只需要下面两步骤：

1
2
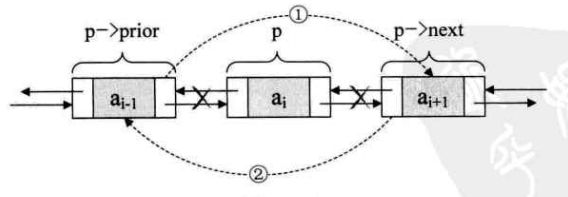
3

p->prior->next = p->next;
p->next->prior = p->prior;
free(p);

好了，简单总结一下，双向链表相对于单链表来说，要更复杂一些，毕竟它多了 prior 指针，对于插入和删除时，需要格外小心。另外它由于每个节点都需要记录两份指针，所以在空间上是要占用多一些的。不过，由于它良好的对称性，使得对某个节点的前后节点的操作，带来了方便，可以有效提高算法的时间性能。说白了，就是用空间来换时间。